ThinkNotes

Simple is not easy

0%

C++ STL类使用笔记

发表于 更新于 分类于

string

find()

查找指定字符串的位置（下标）

string中find()返回值是字母在母串中的位置（下标记录），如果没有找到，那么会返回一个特别的标记npos。（返回值可以看成是一个int型的数）

//find函数返回类型 size_type
string s("1a2b3c4d5e6f7jkg8h9i1a2b3c4d5e6f7g8ha9i");
int position;
//find 函数 返回jk 在s 中的下标位置
position = s.find("jk");
if (position != s.npos)  //如果没找到，返回一个特别的标志c++中用npos表示
{
    printf("position is : %d\n" ,position);
}
else
{
    printf("Not found the flag\n");
}

##查找某字符首次出现，或最后出现的位置
find_first_of() 和 find_last_of()返回子串出现在母串中的首次出现的位置，和最后一次出现的位置
查找上面示例的’c’的下标：

flag = "c";
position = s.find_first_of(flag);
printf("s.find_first_of(flag) is :%d\n",position);
position = s.find_last_of(flag);
printf("s.find_last_of(flag) is :%d\n",position);

image-20221208171122674

查找某给定位置后的子串的位置

//从字符串s 下标5开始，查找字符串b ,返回b 在s 中的下标
position=s.find("b",5);
cout<<"s.find(b,5) is : "<<position<<endl;

查找所有子串在母串中出现的位置

//查找s 中flag 出现的所有位置。
flag="a";
position=0;
int i=1;
while((position=s.find(flag,position))!=string::npos)
{
    cout<<"position  "<<i<<" : "<<position<<endl;
    position++;
    i++;
}

map与unordered_map的区别

内部实现

map：
map内部实现了一个红黑树（红黑树是非严格平衡二叉搜索树，而AVL是严格平衡二叉搜索树），红黑树具有自动排序的功能，因此map内部的所有元素都是有序的，红黑树的每一个节点都代表着map的一个元素。因此，对于map进行的查找，删除，添加等一系列的操作都相当于是对红黑树进行的操作。map中的元素是按照二叉搜索树（又名二叉查找树、二叉排序树，特点就是左子树上所有节点的键值都小于根节点的键值，右子树所有节点的键值都大于根节点的键值）存储的，使用中序遍历可将键值按照从小到大遍历出来。

unordered_map:
unordered_map内部实现了一个哈希表（也叫散列表，通过把关键码值映射到Hash表中一个位置来访问记录，查找的时间复杂度可达到O(1)，其在海量数据处理中有着广泛应用）。因此，其元素的排列顺序是无序的。

优缺点以及适用处

map
优点：有序性，这是map结构最大的优点，其元素的有序性在很多应用中都会简化很多的操作。
红黑树结构：内部实现一个红黑书使得map的很多操作在lgn的时间复杂度下就可以实现，因此效率非常的高

缺点： 空间占用率高，因为map内部实现了红黑树，虽然提高了运行效率，但是因为每一个节点都需要额外保存父节点、孩子节点和红/黑性质，使得每一个节点都占用大量的空间

适用处：对于那些有顺序要求的问题，用map会更高效一些

unordered_map：

优点： 因为内部实现了哈希表，因此其查找速度非常的快
缺点： 哈希表的建立比较耗费时间
适用处：对于查找问题，unordered_map会更加高效一些，因此遇到查找问题，常会考虑一下用unordered_map

总结：
两种map性能分析的内存占用比较，就是红黑树 VS hash表的性能比较, 还是unorder_map占用的内存要高。
但是unordered_map查找的时间复杂度低，执行效率要比map高很多。

使用示例

unordered_map的用法和map是一样的，都提供了 insert，size，count等操作，并且里面的元素也是以pair类型来存贮的。但其内部实现是不同的，对使用者来说不可见。

示例（map_and_unordered.cpp）：

#include <iostream>  
#include <unordered_map>  
#include <map>
#include <string>  

using namespace std;  

int main()  
{  
    ////使用{}赋值, 注意：C++11才开始支持括号初始化
    unordered_map<int, string> myMap = {{ 3, "C" },{ 4, "D" }}; 
    //使用[ ]进行单个插入，若已存在键值2，则修改其值
    myMap[1] = "A";  
    myMap.insert(pair<int, string>(2, "B"));//使用insert和pair插入
  
    //遍历输出+迭代器的使用
    //auto自动识别为迭代器类型unordered_map<int,string>::iterator
    auto iter = myMap.begin(); 
    while (iter!= myMap.end())
    {  
        cout << iter->first << "," << iter->second << endl;  
        ++iter;  
    }  
    
    //查找元素并输出+迭代器的使用
    //find()返回一个指向2的迭代器
    auto iterator = myMap.find(2);
    if (iterator != myMap.end())
        cout << endl<< iterator->first << "," << iterator->second << endl;  
     
    return 0;  
}

编译：
image-20221208171339229

结果：
unordered_map：没有按值的大小排序，从最近插入的到最早插入的，依次显示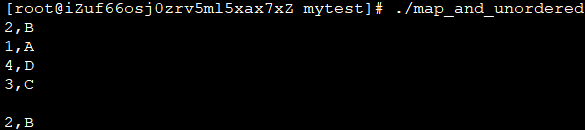
image-20221208171412418
把unordered_map改成map: 按值的大小，从小到大显示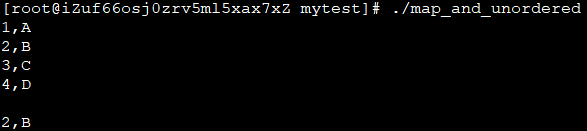
image-20221208171351937

sort

sort()函数是STL中的排序函数，由模板函数实现，复杂度N*logN。该函数专门用来对容器或普通数组中指定范围内的元素进行排序，该函数使用频率较高，且其实现综合了几种经典排序方法
使用格式如下：

sort (first, last) //排序从first到last的数据，默认从小到大
sort (first, last, rule) //以某种规则排序，rule可使用std定义的，或自定义实现

使用示例

几种典型的使用方式：

  • 默认：从小到大
  • greater< Type >()：std提供的从大到小
  • 自定义规则：函数，运算符，Lambda实现，这里规则都是传入两个参数（分别是要比较数组的靠左值，靠右值），返回bool类型，如果左值<右值，即从小到大排序，反之从大到小

代码：

#include <iostream>     // std::cout
#include <algorithm>    // std::sort
#include <vector>       // std::vector
#include <stdlib.h>

using namespace std;

//以普通函数的方式实现自定义排序规则
bool myComp(int i, int j) {
    return (i < j);
}

//以对象的方式实现自定义排序规则
class myCompOper {
public:
    bool operator() (int i, int j) {
        return (i > j);
    }
};

//打印数组
void print_array(std::vector<int> &a, const char *s)
{
    printf("%s\n", s);
    vector<int>::iterator it;
    for (it = a.begin(); it != a.end(); ++it)
    {
        printf("%d ", *it);
    }
    printf("\n");
}

int main() {
    //std::vector<int> array;
    //char num;
    //while(cin.get() != '\n')
    //{
    //    cin >> num;
    //    array.push_back(num);
    //}

    vector<int> array{1,3,4,2,5,7,6,8,9};
    print_array(array, "input array:");

    //默认排序，从小到大
    std::sort(array.begin(), array.end());
    print_array(array, "default sort:");

    //使用STL标准库提供的其它比较规则, 比如 greater<T>，从大到小
    std::sort(array.begin(), array.end(), std::greater<int>());
    print_array(array, "std::greater<T> sort:");

    //自定义比较规则: 普通函数
    std::sort(array.begin(), array.end(), myComp);
    print_array(array, "myComp sort:");

    //自定义比较规则: 类内运算符重载
    std::sort(array.begin(), array.end(), myCompOper());
    print_array(array, "myCompOper sort:");

    //自定义比较规则: Lambda匿名函数
    std::sort(array.begin(), array.end(), [](int i, int j) {return i < j;});
    print_array(array, "Lambda sort:");

​
return 0;
}

结果如下：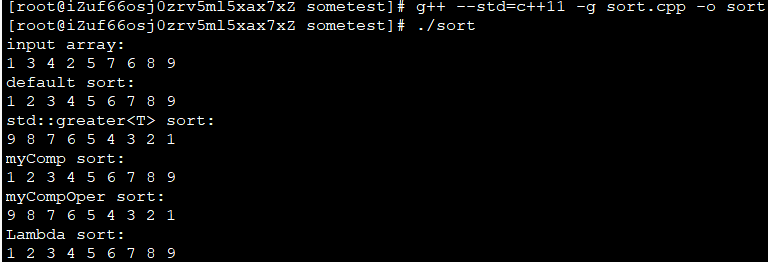
image-20221208171536663

内部实现

STL中的sort并非只是普通的快速排序，除了对普通的快速排序进行优化，它还结合了插入排序和堆排序。根据不同的数量级别以及不同情况，能自动选用合适的排序方法。当数据量较大时采用快速排序，分段递归。一旦分段后的数据量小于某个阀值，为避免递归调用带来过大的额外负荷，便会改用插入排序。而如果递归层次过深，有出现最坏情况的倾向，还会改用堆排序。

(1)普通快排
普通快速排序算法可以叙述如下，假设S代表需要被排序的数据序列：

  • 如果S中的元素只有0个或1个，结束。
  • 取S中的任何一个元素作为枢轴pivot。
  • 将S分割为L、R两端，使L内的元素都小于等于pivot，R内的元素都大于等于pivot。
  • 对L、R递归执行上述过程。

快速排序最关键的地方在于枢轴的选择，最坏的情况发生在分割时产生了一个空的区间，这样就完全没有达到分割的效果。STL采用的做法称为median-of-three，即取整个序列的首、尾、中央三个地方的元素，以其中值作为枢轴。

分割的方法通常采用两个迭代器head和tail，head从头端往尾端移动，tail从尾端往头端移动，当head遇到大于等于pivot的元素就停下来，tail遇到小于等于pivot的元素也停下来，若head迭代器仍然小于tail迭代器，即两者没有交叉，则互换元素，然后继续进行相同的动作，向中间逼近，直到两个迭代器交叉，结束一次分割。

(2)内省式排序 Introsort
不当的枢轴选择，导致不当的分割，会使快速排序恶化为 O(n2)。David R.Musser于1996年提出一种混合式排序算法：Introspective Sorting（内省式排序），简称IntroSort，其行为大部分与上面所说的median-of-three Quick Sort完全相同，但是当分割行为有恶化为二次方的倾向时，能够自我侦测，转而改用堆排序，使效率维持在堆排序的 O(nlgn)，又比一开始就使用堆排序来得好。

sort声明：

#include <algorithm>
 
template< class RandomIt >
void sort( RandomIt first, RandomIt last );
 
template< class RandomIt, class Compare >
void sort( RandomIt first, RandomIt last, Compare comp );

sort实现：

template <class _RandomAccessIter>
inline void sort(_RandomAccessIter __first, _RandomAccessIter __last) {
  __STL_REQUIRES(_RandomAccessIter, _Mutable_RandomAccessIterator);
  __STL_REQUIRES(typename iterator_traits<_RandomAccessIter>::value_type,
                 _LessThanComparable);
  if (__first != __last) {
    __introsort_loop(__first, __last,
                     __VALUE_TYPE(__first),
                     __lg(__last - __first) * 2);
    __final_insertion_sort(__first, __last);
  }
}

__introsort_loop便是上面介绍的内省式排序，其第三个参数中所调用的函数__lg()便是用来控制分割恶化情况，求lg(n)（取下整），意味着快速排序的递归调用最多 2*lg(n) 层。
__lg()实现如下

template <class Size>
inline Size __lg(Size n) {
    Size k;
    for (k = 0; n > 1; n >>= 1) ++k;
    return k;
}

__introsort_loop实现：

  • 首先判断元素规模是否大于阀值__stl_threshold，__stl_threshold是一个常整形的全局变量，值为16，表示若元素规模小于等于16，则结束内省式排序算法，返回sort函数，改用插入排序。
  • 若元素规模大于__stl_threshold，则判断递归调用深度是否超过限制。若已经到达最大限制层次的递归调用，则改用堆排序。代码中的partial_sort即用堆排序实现。
  • 若没有超过递归调用深度，则调用函数__unguarded_partition()对当前元素做一趟快速排序，并返回枢轴位置。
  • 经过一趟快速排序后，再递归对右半部分调用内省式排序算法。然后回到while循环，对左半部分进行排序。源码写法和我们一般的写法不同，但原理是一样的，需要注意。

递归上述过程，直到元素规模小于__stl_threshold，然后返回sort函数，对整个元素序列调用一次插入排序，此时序列中的元素已基本有序，所以插入排序也很快。至此，整个sort函数运行结束。

__introsort_loop代码：

template <class _RandomAccessIter, class _Tp, class _Size>
void __introsort_loop(_RandomAccessIter __first,
                      _RandomAccessIter __last, _Tp*,
                      _Size __depth_limit)
{
  while (__last - __first > __stl_threshold) {
    if (__depth_limit == 0) {
      partial_sort(__first, __last, __last);
      return;
    }
    --__depth_limit;
    _RandomAccessIter __cut =
      __unguarded_partition(__first, __last,
                            _Tp(__median(*__first,
                                         *(__first + (__last - __first)/2),
                                         *(__last - 1))));
    __introsort_loop(__cut, __last, (_Tp*) 0, __depth_limit);
    __last = __cut;
  }
}

__unguarded_partition()函数

template <class _RandomAccessIter, class _Tp>
_RandomAccessIter __unguarded_partition(_RandomAccessIter __first, 
                                        _RandomAccessIter __last, 
                                        _Tp __pivot) 
{
    while (true) {
        while (*__first < __pivot)
            ++__first;
        --__last;
        while (__pivot < *__last)
            --__last;
        if (!(__first < __last))
            return __first;
        iter_swap(__first, __last);
        ++__first;
    }
}

参考： 《STL源码剖析》–侯捷